本文的讨论是将九句因和我们现代人熟悉的集合论结合起来,试图找到简易的方式,便于现代教育背景的学人快速理解和记忆九句因的要义。
九句因是因明中同品和异品与因的九种关系。它是明因三相说的理论基础,也是新因明三支作法的理论基础。首见于陈那论师的《因明正理门论》和《因轮论》。原为分析因与同品、异品诸种关系的,但反过来也成了检查因的正或不正(错误)的方法。 我们为了更好地理解和掌握九句因,采用现代人所熟知的集合文氏图表达方法给予表述。
我们的讨论要利用集合论的一些知识,涉及集合的基本概念在这里先复习一下(中学内容,还记得的同学请跳过下面一节内容):
1. 相关定义
1.1. 集合
是指由指定范围内的满足给定条件的所有对象聚集在一起构成,每一个对象称为这个集合的元素。用x表示元素,A表示集合,有:x ∈ A(读作:x属于A)
我们所有描述性语言都是把事相和属性相关联。属性,就是约束(给集合划范围,范围内所有满足属性的对象被称为元素,这里用x表示,A表示集合)
1.2. 全集
针对一个具体范围,我们考虑的所有对象的集合叫做全集(universal set),记作U,在文氏图一般使用方形表示全集。
示例:
在立体几何(一个空间)中,全集是由空间的全体点(所有空间的点)组成的;在我国的人口普查中,全集是由我国所有人组成的(对世界人口来说就是个子集了)。
在不同场景下,可能采用不同全集。在因明讨论中,有一个重要的全集概念:有实法。
1.3. 包含关系
子集和真子集
设A、B是任意两个集合,如果B的每个元素都是A中的元素,则称B是A的子集,也称做B被A包含或A包含B,记作B ⊆ A,否则记作B ⊈ A。
如果B ⊆ A并且A!= B,即排除A=B这一情况,则称B是A的真子集,也称做B被A真包含或A真包含B,记作B ⊂ A。即:如果B包含于A,且B不等于A,就说集合B是集合A的真子集。
比如:白马是马的真子集。(白马属于马,但马的概念大于白马,还有红马、黑马等等)
“⊆”关系的数学语言描述为:B⊆ A ⇔对∀x,如果x ∈ B,则x ∈ A。(∀符号表示“所有的”)(“=>”读为“推出”,“⇔”读为“等价于”)
1.4. 文氏图
文氏图就是用一条封闭线直观地表示集合及其关系的图形,它能直观地表现出集合之间的关系。封闭线内包含的点代表对应描述集合的元素。如下图:
所有的马:
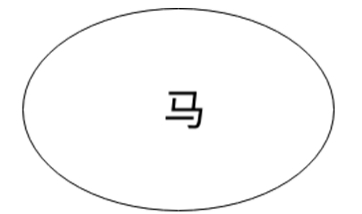
用文氏图表示包含关系:
外圈是马,小圈是白马。说明除了白马还有其他类型的马。

1.5. 全集、补集
全集是一个相对的概念,只包含所研究问题中所涉及的所有元素(和我们研究的问题有关),补集只相对于相应的全集而言。如:我们在整数范围内研究问题,则Z为全集,而当问题拓展到实数集时,则R为全集,补集也只是相对于此而言。
因明九句因经常讨论的全集往往以有实法(有功用的法)作为全集,比较广泛。这里是说,看你研究什么问题,比如你研究人,那么人类是你全集。
补集一般指绝对补集,即一般地,设U是全集合,A是U的一个子集,由U中所有不属于A的元素组成的集合,叫做子集A在U中的绝对补集。
补集是以全集为基础,抠掉你描述的集合。

所有的马为全集U,白马是其一个子集,白马的补集,即除白马以外的其他颜色的马,如上图所示,图中为“马”的全集,“抠除”“白马”的部分后剩余的部分。
因明讨论中通常暗设了讨论的全集为一切有实法。
2. 因明和集合论基本的对应描述
因和宗通过描述性的语言清晰地指向一个集合(分别指向一个集合),我们可以这样对描述语言进行等价:
声是无常,所作故。
首先,声是所作的,即是说声这个元素(或者说子集)属于所作的法这个集合。用x代表所有声音,有所有的声音属于所作的法,集合用A表示。就有x∈ A。
有法,要在因上成立。话里涉及的主体,描述对象(有法),即声音,它首先得是所作的。否则不用再继续推理了。声这个元素,属于所有所作法的集合。
所作故,所作的所有法。
无常,描述成无常的法,这也是由所有无常的法组成的集合(宗的集合),记为B。
由于存在公理——造作的法都是无常的法(涉及到边界问题,定义的约束是边界,比如无常,所作),即所有的造作的法都属于无常的法(这个是一个公理,现量支撑。当然这个公理正是要用九句因观察的对象),记为∀x∈A =>∀x∈B,即集合A⊆B,那么x∈ B,得到结论:所有的声音属于无常的法,即声是无常。
整理一下等价说法:
无常<=>无常的法组成的集合,记为B;
所作<=>所作的法组成的集合,记为A;
声是无常<=>声音属于无常的法这个集合,记为x∈B;
所作故<=>原因是:声音属于造作的法,记为x∈A;
声是无常,所作故<=>因为x∈A,并且A⊆B(因包含于宗),所以x∈B。
对应因明中立宗和因的描述:有法对应元素;立宗,是将某个元素和属性相关联,即是在说某个元素有什么样的属性,对应上面的描述也等价于,某个元素属于某个满足属性的集合。比如声是无常。是说声音作为一个元素,具有无常的属性,它属于无常法这个大集合。对因的描述也是同样的,如:声是无常所作故。所作故是说因,完整描述是“因为声音是所作的,所以声音是无常的。”因的完整描述是:声音是所作的。也就是说声音具有所作的属性,属于所作法这个集合。
3. 九句因
好了,上面复习了这么多集合方面的知识,现在回到本文主要想说明的九句因上来。我们尝试用文氏图直观表达九句因的逻辑关系。
对应我们上述的集合描述方式。设:
A——因;
B——宗;
U——全集(矩形表示)
注意:九句因是按照宗在因和宗的异品(补集)在因上的包含关系进行观察,即同品观察B是否包含于A,B⊆A。异品观察CuB是否包含于A,CuB⊆A。
3.1. 同品全有,异品全有;(不定)
宗的同品,就是宗这个集合以内的所有元素。异品全有,不属于宗的所有元素,当然是在全集之内,也属于因这个集合。即是A=U的情况,A是全集,B是真子集。文氏图如下图所示:

这里对同品和异品的观察做个详细阐述,后面的推导类同。
首先观察宗(集合B)的同品,即是B这个集合的所有元素,用图表示如下:

观察同品是否全有,既是看B上的元素是否全属于A,图上的观察方式是看A是否完全覆盖B,显然这里的图是这样的。
观察异品是否全有,及时看全集抠掉B这个区域(如下图所示的蓝色区域)上的元素是否全属于A,图上看A是否完全覆盖蓝色区域,从这里的图看,也是这样。所以该图准确表达了同品全有,异品全有的逻辑关系。后面几种情况作类似分析,不再赘述。

对此举例说明:这匹是白马,它是马之故。有法:这匹(动物),因:是马,宗:是白马。当然这是个不定因。
大家注意一点,在我们习惯的逻辑推导中,比如三段论、三相推理等,一个因若要称为真因,观察的着眼点是:因必须遍成立于宗(因成立,宗一定成立)。这里的着眼点是看宗和宗的异品是否遍于因,而不是因遍于宗,这是容易混淆的点。
3.2.同品全有,异品没有;(因和宗的集合相等)
——真因之一
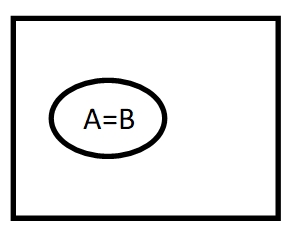
A描述所有地球和环地球轨道上的人类,B描述吸氧的人类,两个描述指向了相同的对象。我们观察B是否包含于A。B属于A没问题,B外面的东西完全不属于A,这个就是同品全有,异品没有,即A=B。
3.3. 同品全有,异品部分有;(不定)

B(宗)包含于A(因) 。
B(宗)的补集在A(因) 上有一部分。
3.4. 同品没有,异品全有;(相违)

B(宗)一点不包含于A(因) ,B(宗)的补集全属于A(因)。
3.5. 同品没有,异品没有;(不定)
其实这个情况是说宗和宗的异品都和因没有任何交集,那么,宗和宗的补集之和构成的全集与因没有交集,换句话说就是因在全集之外,显然违背了全集的定义,这本身是一个逻辑矛盾,因此画不出文氏图。
现代逻辑中的排中律(排中律定义:逻辑的取值只能是真或假,没有中间状态)说的就是此类情况不成立。
3.6. 同品没有,异品部分有;(相违)
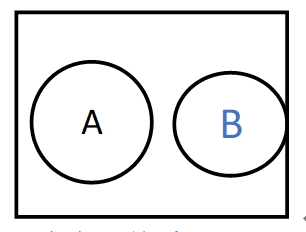
没有交叉关系;B(宗)一点都不属于A(因) ,B(宗)的补集只有一部分在A里。
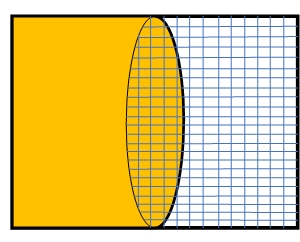
3.7. 同品部分有,异品全有;(不定)
A:黄色部分(因) ;B:网格部分(宗)。
网格区域以外,全属于黄色。
3.8. 同品部分有,异品没有;
——真因之二
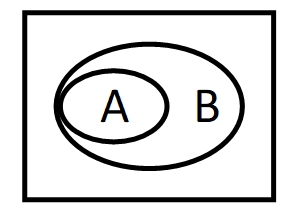
B(宗)有一部分包含于A(因)。B(宗)的补集完全和A(因) 没有交集。
3.9. 同品部分有,异品部分有;(不定)
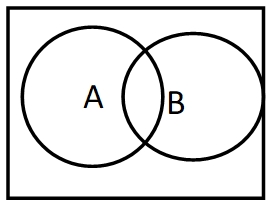
B(宗)有一部分包含于A(因)。B(宗)的补集有一部分包含于A(因)。
小结:
1)真因只有2和8两种:
A(因) =B(宗)
A(因) ⊂ B(宗)
这两种情况加起来,就是因包含于宗(A ⊆B)。包含于——真包含和等于加起来。
2)除了真因,和自带矛盾的第5种情况,从图中能够一眼看出是相违还是不定。A和B有交集的为不定因;A和B没有交集的为相违因。
3)真因都是异品没有,而异品没有不是真因的情况很好辨认,因为其违背排中律,因此我们能以此快速确定真因。
4)有了上述工具,我们在分析具体问题时,可以通过对照上述文氏图,快速确定问题属于哪种情况。
4. 九句因中“九”种情况是完备的
同品和异品两种分类,出现三种情况,组合就是九种,是完备的,讨论了所有情况。
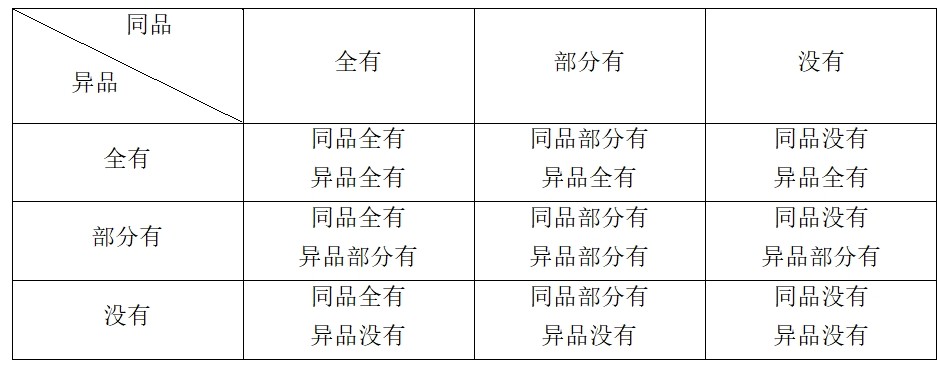
5. 拓展:三段论立论形式和因明立论形式的对照
说到逻辑定然绕不开三段论这个词汇。所谓三段论,简单来说,是一种以“大前提+小前提+结论”为结构的逻辑推理方式。
著名的“苏格拉底三段论”——
大前提:所有人都是要死的;
小前提:苏格拉底是人;
结论:所以苏格拉底是要死的。
那我们来看看怎么对应到我们的有法、宗、因上面来。针对上述话题应该有:
有法:苏格拉底;
因:是人;
宗:会死。
小前提说:苏格拉底是人,其实在因明里的描述方式是:有法在因上成立。
大前提:所有人都是要死的。表达的是九句因的第八项(此例如此,当然第二项也可以作为大前提),当然是一个真因。作此对比便于我们认清不同语言表达下的相同逻辑内核。同时也可看到,九句因的分析方式非常详尽。